جدوع: المجالات في مجموعة الأعداد الحقيقية

في هذا الدرس نتعرف على المجالات في مجموعة الأعداد الحقيقية وعلى أنواعها و طريقة تمثيلها على المستقيم العددي. في مرحلة ثانية نتطرق إلى إتحاد و تقاطع المجالات في مجموعة الأعداد الحقيقية.
فهرس الدرس :

1. ماهو المجال ؟
2. تمثيل المجال على المستقيم المدرج
3. أنواع المجالات
4. تقاطع مجالين
5. إتحاد مجالين
6. تمارين محلولة

ماهو المجال ؟

المجال في مجموعة الأعداد الحقيقية هوجميع الأعداد المحصورة بين عددين حقيقين. مثلا المجال [ 6 ; 1 ] هو جميع الأعداد الحقيقية المحصورة بين 1 و 6. ونكتب : 

• نقرأ المجال [ 6 ; 1 ] هو جميع الأعداد الحقيقية  المحصور بين 1 و6 بما فبها 1 و6. 
• العددان 1 و 6 يسميان محداي المجال [ 6 ; 1 ] ( بمعنى طرفي المجال ).
• عندما نكتب ] 6 ; 1 ] هذا يعني أننا نتحدث عن جميع الأعداد المحصورة بين 1 و 6 و ( 1 ينتمي إلى المجال

] 6 ; 1 ] و 6 لا تنتمي إلى المجال ] 6 ; 1 ])

• عندما نكتب [ 6 ; 1 [ هذا يعني أننا نتحدث عن جميع الأعداد المحصورة بين 1 و 6 و ( 1 ينتمي إلى المجال

[ 6 ; 1 [ و 6 لا تنتمي إلى المجال ]  6 ; 1 ]) 

تمثيل المجال على المستقيم العددي ( المستقيم المدرج) :

نأخـــد مثلا المحدين 1 و 2 في المجالات : [ 2 ; 1 ] و ] 2 ; 1 [  و [ 2 ; 1  [  و ]  2 ; 1 ]
ونستعرض مختلف التمثيلات على المستقيم العددي.

المحدات :	المحد 1		المحد  1
	يتتمي 1	لاينتمي 1	لاينتمي 2	يتتمي 2
المتفاوتة :	x ≥ 1	x > 1	x < 2	x ≤ 2
تمثيلها على مستقيم مدرج :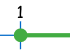
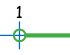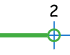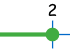ترميز المجال :	1]	1[	]2	[2

تمرين محلول :
قم بمسك وتحريك النقطتين الحمراء والبنفسجية على الخط المتقطع لتغيير ترميز المجال و النقطتين الخضراءو الزرقاء لتغيير محدي المجال. ثم تأكد من صحة جوابك بوضع علامة صح في المربع الصغير: ' تأكد من صحة الجواب' :

أنواع المجالات

نلخص أنواع المجالات في مجموعة الأعداد الحقيقية.
المجالات المحدودة :

المجالات الغير محدودة :

أمثلة:

[ a ; b ] : مجال مغلق
] a ; b [ : مجال مفتوح
[ a ; b [ و  ] a ; b ] : مجال نصف مفتوح ( أو نصف مغلق ) 

تقاطع المجالات

تقاطع المجالين [ a ; b ]  و [ c ; d ] هي مجموعة الأعداد الحقيقية التي تنتمي إلى المجالين [ a ; b ]
  و [ c ; d ] في نفس الوقت.

إذا كان هو تقاطع المجالين [ a ; b ]  و [ c ; d ] نكتب :

مثال 1 :

مثال 2 : 
يمكننا بإستعمال المستقيم المدرج تحديد تقاطع مجالين كما في المثال التالي :

إتحاد المجالات

إتحاد المجالين [ a ; b ]  و [ c ; d ] هي مجموعة الأعداد الحقيقية التي تنتمي إلى المجالين [ a ; b ]
  أو [ c ; d ] .

إذا كان هو إتحاد المجالين [ a ; b ]  و [ c ; d ] نكتب :

مثال 1 :

مثال 2 :

البرمجية التالية تمكنك من تحديد تقاطع و إتحاد مجالين ، ما عليك سوى مسك وتحريك النقطتين الحمراء و الخضراء على الخط المتقطع  لتحديد المجالين ثم إضغط إظهار أو إخفاء التقاطع أو الإتحاد بحسب رغبتك: