القيمة المطلقة لعدد حقيقي هي المسافة بين النقطة التي أفصولها هذا العدد الحقيقي و النقطة التي أفصولها هو 0. عندما يقال لك حل معادلة تتضمن القيمة المطلقة فالمطلوب منك في مرحلة أولى التخلص من رمز القيمة المطلقة بإعتماد التعريف و من تم حل المعادلة إذا كانت تقبل حلولا . فيما يلي تذكير سريع بتعريف القيمة المطلقة مرفوق بتمارين محلولة تتضمن القيمة المطلقة :
أمثلة لمعادلات تتضمن القيمة المطلقة في حالات بسيطة :
تذكير :
ملاحظات أساسية
- القيمة المطلقة دائما تكون موجبة.
- يكون عددان حقيقيان لهما نفس القيمة المطلقة إذا و فقط إذاكانا متقابلين.
- القيمة المطلقة لعدد سالب هي مقابل هذا العدد.
- القيمة المطلقة لعدد موجب هي العدد نفسه.
1. حل المعادلة :

هذه المعادلة لا حل لها لأن العدد 1- سالب و (القيمة المطلقة دائما تكون موجبة). و منه :
في البرمجية التالية يمكنك معاينة مجموعة من المعادلات من هذا النوع، ضع عامة صح في الخانة أو أطلب معادلة جديدة :
أمثلة لمعادلات تتضمن القيمة المطلقة في حالة الجمع :
لكي نحل هذه المعادلة المطلوب التخلص من رمز القيمة المطلقة في حدي الفرق في الطرف الأيسر من المعادلة، لهذا سنقوم بما يلي :
- x - 5 = 2 مع x من المجال [3- ; -
 [ : تعني أن x = 7 لا يمكن
[ : تعني أن x = 7 لا يمكن - 3x + 1 = 2 مع x من المجال [1 ,3-[ : تعني أن x = 1/3 يمكن
- x + 5 = 2- مع x من المجال ]
 + ; 1[ : تعني أن x = 3 يمكن
+ ; 1[ : تعني أن x = 3 يمكن








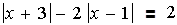




1 تعليقات على موضوع "طريقة حل معادلة تتضمن القيمة المطلقة"
اريد حل هده المسالة
ليكن x عدد حقيقي وpx عبارة معرفة كما يلي px
الإبتساماتإخفاء