جدوع: الحسـاب المثلثي : النسب المثلثية في المثلث القائم الزاوية (تذكير)

في هذا الدرس سنتعرف على النسب المثلثية في المثلث القائم الزاوية ونتطرق إلى الثلاثي الشهير جيب زاوية sin ، جيب تمام زاوية cos و ظل زاوية tan .

1 - المثلث القائم الزاوية :

تذكير

ABC مثلث قائم الزاوية في A.

[AB] : هو الضلع المقابل للزاوية θ

[AC] : هو الضلع المحاذي للزاوية θ 

[BC] : هو الوتر.

مبرهنة فيتاغورس :

 في مثلث قائم الزاوية مربع الوتر يساوي مجموع مربعي طولي الضلعين الاخرين.

ABC مثلث قائم الزاوية في A يعني ان :BC² = AB² + AC².

2- النسب المثلثية في المثلث القائم الزاوية :

ليكن ABC مثلث قائم الزاوية في A.

ماهي النسب المثلثية ؟ ولماذا أطلق عليهاهذا الاسم؟

نعلم ان النسبة في أبسط صورها هي مقارنة بين مقدارين مثلاً النسبة بين طول مستطيل وعرضه إذا كانت تساوي 3/2
تعني أنه إذا كان طول المستطيل هو 6 سنتمتر فإن عرضه سيكون هو4 لأن :6/4 = 3/2
في المثلث سنحسب النسب AB/BC و AC/BC و AB/AC للزاوية °30. 

قم بتغيير قيم أطوال اضلاع المثلث و ذالك بمسك و تحريك النقطة A ثم دون ملاحظاتك بخصوص النسب AB/BC و AC/BC و AB/AC للزاوية °30. قم بتغيير قياس الزاوية °30 بزاوية أخرى من خلال القائمة الأفقية وكرر العمل ... ماذا تلاحـــظ؟

ما هي ملاحظاتك عندما تثبت قياس الزواية θ و تغيير أطوال أضلاع المثلث؟

لا شك انك لاحظت ان هذه النسب تبقى تابثة مهما نغير في اطوال اضلاع المثلث ABC.
هذه النسب الثلاث تسمى النسب المثلثية في المثلث القائم الزاوية. وهو الثلاثي المشهور ب sin و cos و tan.

في المثلث ABC القائم الزاوية في A : يمكن ان نجد النسب AB/BC و AC/BC و AB/AC وهناك ثلات نسب بين أطوال أضلاع هذا المثلث هي مقلوبات هذه النسب ( يمكنك أن تجدها بنفسك إن أردت.

 سميت هذه النسب باسم النسب المثلثية لأنها تقارن بين أطوال أضلاع مثلث قائم الزاوية بالتحديد، ولكن هذه النسب ترتبط أيضا بزوايا المثلث ولهذا أعطاها علماء الرياضيات أسماءً مربوطة بزوايا المثلث كما سنتعرف في ما سيأتي :

 

1 - جيب الزاوية : Sinus

النسبة الأولى تسمى جيب الزاوية θ وهي تحسب كما يلي :

نرمز لجيب الزاوية θ ب : ( sin( θ ونقرأ جيب الزاوية θ و نكتب  sin( θ ) = AB/BC

بصفة عامة : 

 جيب زاوية هو خارج طول الضلع المقابل للزاوية على الوتر.

 2 - جيب الزاوية تمام : Cosinus

النسبة الثانية تسمى جيب تمام الزاوية θ وهي تحسب كما يلي :

نرمز لجيب الزاوية تمام θ ب : ( cos( θ ونقرأ جيب تمام الزاوية θ و نكتب  cos( θ ) = AC/BC

بصفة عامة : جيب زاوية تمام هو خارج طول الضلع المحاذي للزاوية على الوتر.

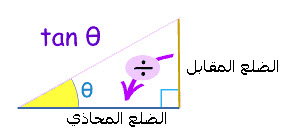
3 - ظل الزاوية : Tangente  

النسبة الثالثة تسمى ظل الزاوية θ وهي تحسب كما يلي :

نرمز لظل الزاوية θ ب : ( tan( θ ونقرأ ظل الزاوية θ و نكتب  tan( θ ) = AB/AC

بصفة عامة : ظل زاوية هو خارج طول الضلع المقابل للزاوية على الضلع المحاذي.

SOH و CAH و TOA.

لعلكم تتساؤلون عن معنى هذه الكلمات الثلاث التي أوردتها في العنوان  ... هل هي أيضا نسب مثلثية ؟

لا ... هذه الكلمات ليست نسب مثلثية لكنها ستساعدنا على ضبط العلاقات و التحكم في النسب المثلثية و في طريقة إستعمالها لتحديد طول ضلع مجهول في مثلث قائم الزاوية أو تحديد قياس زاوية إذا كنا نعلم طولي ضلعين في المثلث القائم الزاوية.

لنأخد الكلمة SOH و نحاول أن نتعرف على معناها وكيف يمكننا الإستفادة من هذه الكلمة و التي تتشكل من 3 حروف فقط.

تعلمون أن المثلث القائم الزاوية يشتمل على 3 أضلاع و إذا كانت θ زاوية في المثلث فإننا يمكن أن نتحدث عن الضلع المقابل للزاوية  θ و الضلع المحاذي للزاوية θ ثم الوتر. لهذا دعونا نعرج أولا على جدول للمصطلحات حتى نتمكن من فك لغز هذه الكلمات الغريبة .

المصطلح باللغة العربية	المصطلح باللغة الفرنسية	الحرف الأول في الكلمة بالفرنسية
جيب	Sinus	S
جيب تمام	Cosinus	C
ظل	Tangente	T
الضلع المقابل	Le coté Opposé	O
الضلع المحاذي	Le cote Adjacent	A
الوتر	L'Hypoténuse	H

كما تلاحظون فكلمة SOH تتشكل من أوئل حروف الكلمات Sinus و Opposé و Hypoténuse . و بالتالي إذا حفظنا الكلمة سنتمكن من حفظ علاقة جيب زاوية بأطوال الأضلاع في المثلث القائم الزاوية الواردة في بداية الدرس :

جيب زاوية ( S )  هو خارج طول الضلع المقابل ( O ) للزاوية على الوتر ( H )

جيب تمام زاوية ( C )  هو خارج طول الضلع المحاذي ( A ) للزاوية على الوتر ( H )

ظل زاوية ( T )  هو خارج طول الضلع المقابل ( O ) للزاوية علىطول الضلع المحاذي  ( A )

وهكذا بالنسبة للكلمتين : CAH و TOA
البرمجية التالية تساعدك على تثبيت و فهم الامر و التمكن من الطريقة و إستغلالها أحسن إستغلال . تتبع التعليمات الواردة :